机器学习

基础概念

流程

雕刻：决定项目内容，界定范围

收集数据，确认标签

训练，错误分析，迭代

监控性能，维持

监督学习和非监督学习

前者给出明确数据集，后者自动优化算法实现分类

多类特征

上标 i 说明是第几组数据（一个列表），下标 j 是一组数据中的第几个的特征值

特征缩放

通过对数据权重的缩放来保证机器学习的合理性

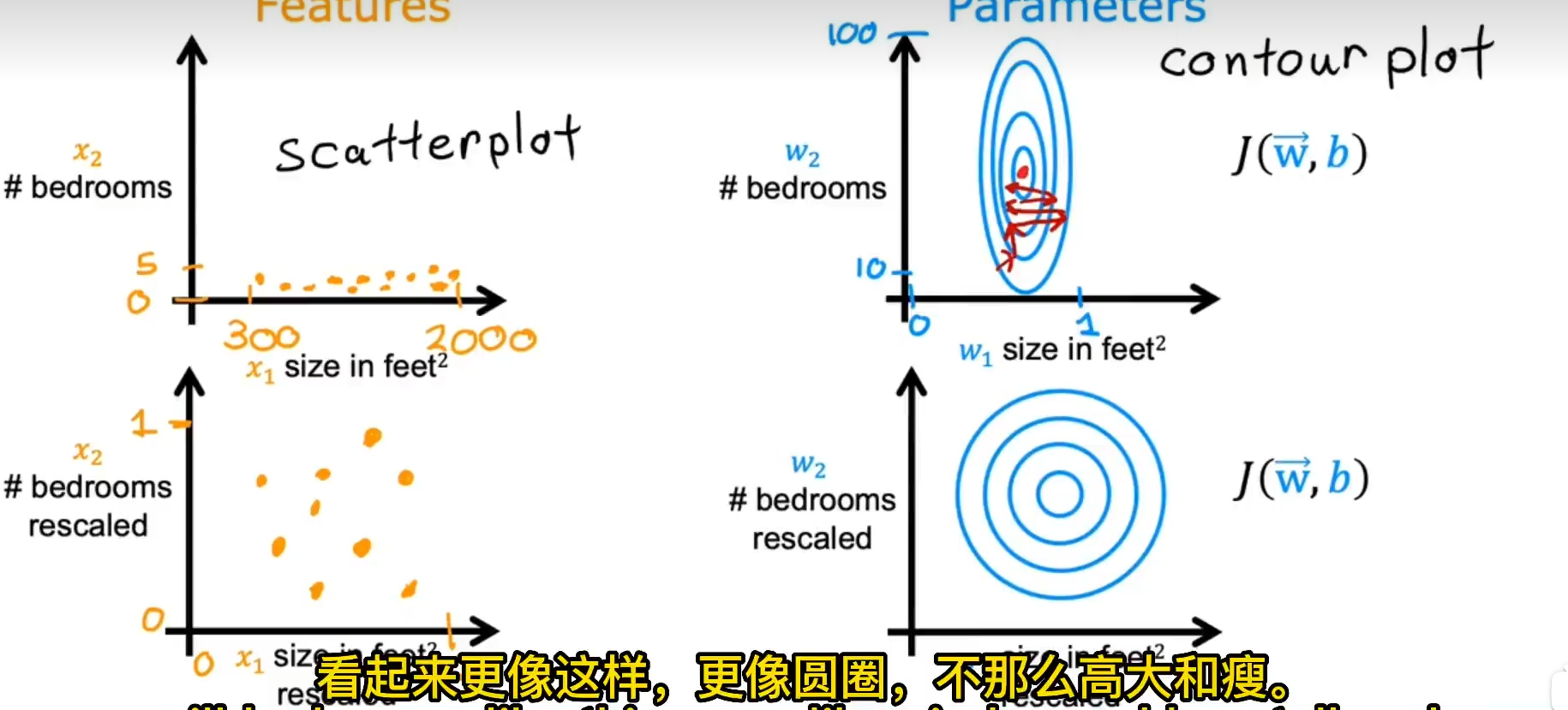
例如上图数据，x1 权重高导致 x 的轻微改变都会导致数据变化过大，从而成本函数等高线图是一个椭圆，梯度下降难以进行，总体上让数据接近 1

方法：

除以最大值

均值归一 减去平均值然后除以最大最小值的差

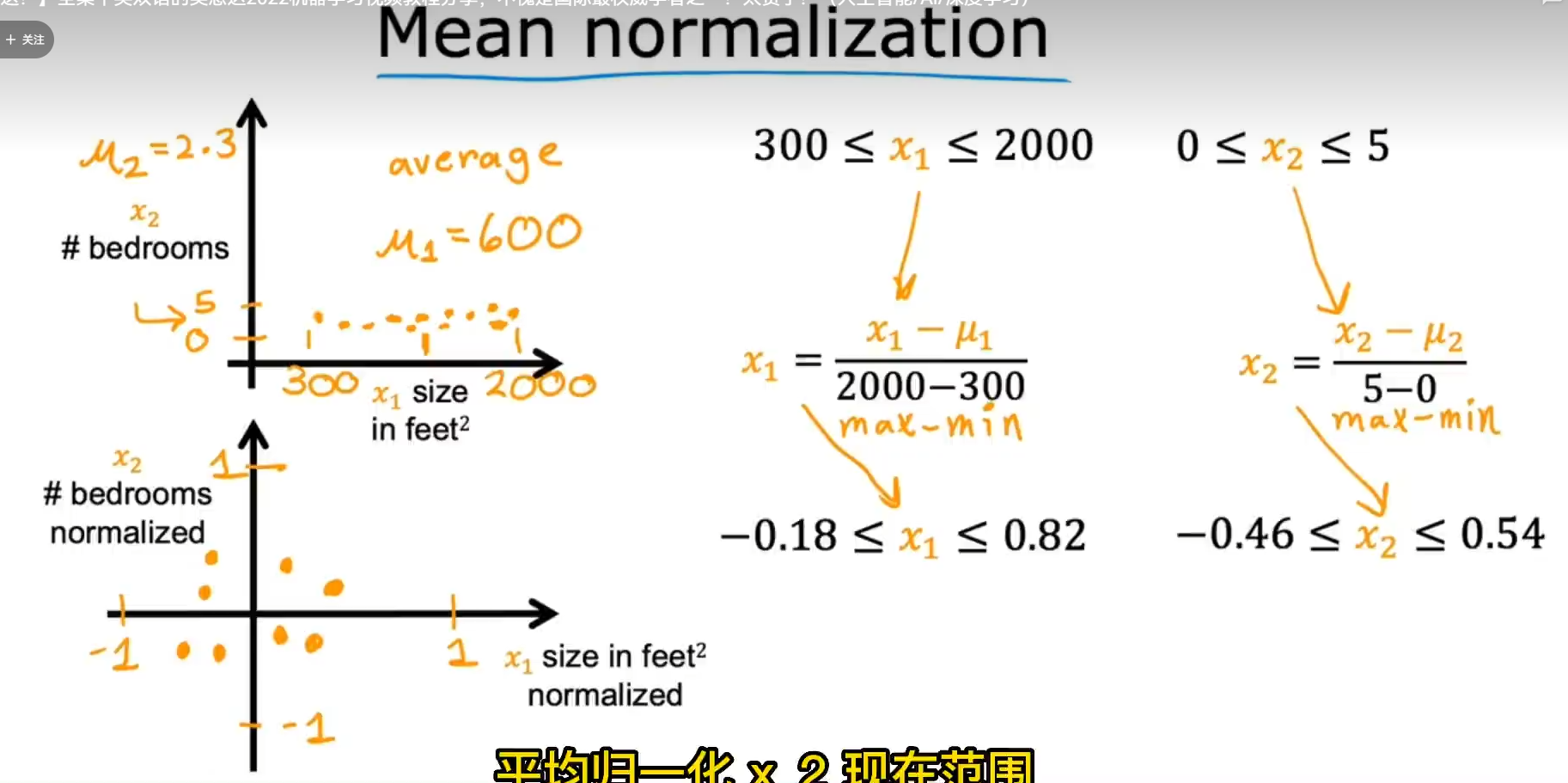
z-score 归一化 减去平均值除以标准差

特征工程

例如房子使用 wx1+wx2+b 来估测，x1 与 x2 是长和宽 可以建立一个 x3 为面积 然后用 w3+wx1+wx2+ 估测

数据增强

改变数据（例如旋转图片，给图片加底噪）来增大数据集

基线

选择一个值来作为误差的参考值，例如识别图像时人的正确率

迁移学习

利用已经训练过的神经网络，通过改变输出层的参数或者改变所有参数来应用于自身的模型

误差度量

例如现在有一个罕见的疾病，其发生率是百分之零点五，如今有多个算法，其中一个算法永远输出“没有疾病”，他的误差就只有百分之零点五，但是显然这个算法是没有意义的

精度：成功预测病人有病/共预测病人有病数量

(预测的病人大概率是真的）

召回：成功预测病人有病/真实病人有病数量

（有病的病人大概率被预测出来）

逻辑回归：当门槛升高，意味着需要更高的预测值才会判断有病，这会导致精度更高，同时召回更低

计算 f1 score（调和平均数），较小的数据会导致分母过大，然后去总体大的数据

监督学习算法

线性回归

w 变化率，b 常数

逻辑回归

决策边界：wx+b＝0 也就是令 sigmoid 函数的参数为零，通过选择更合适的 z 函数会使得决策边界更加合理，从而良好的预测数据

g：sigmoid function

softmax 回归

神经网络

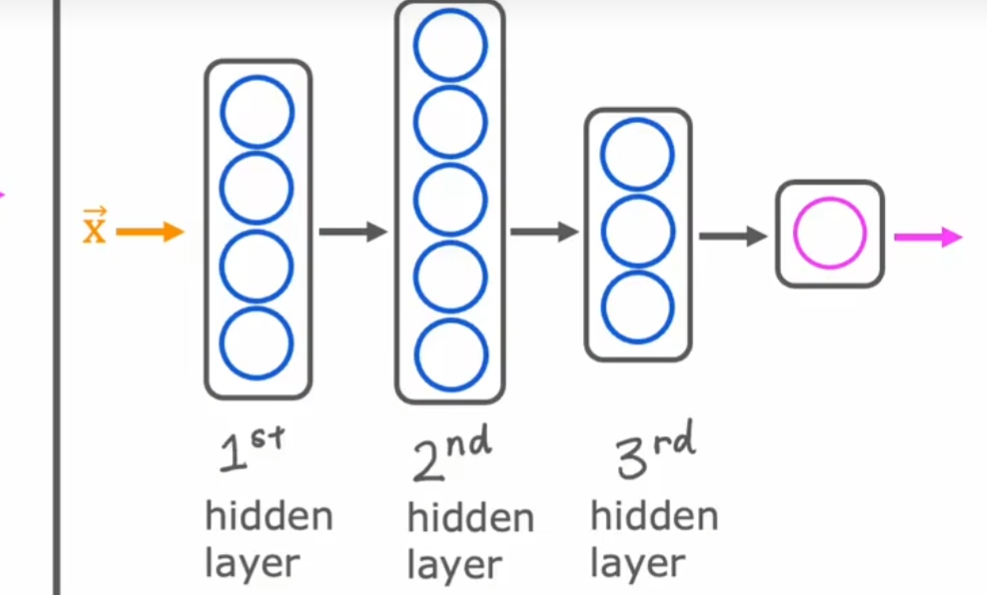
（输入层）特征向量 x 在隐藏层的作用下变成了激活值（此过程是多次重复的，次数取决于有几个隐藏层，输出的激活值个数取决于这一层中有多少个神经元，其本质类似于特征工程，是通过特定小逻辑回归（g 是 sigmoid function 也叫做激活函数，也可以是其他算法）

单元/函数将输入的向量转化为几个激活值，例如：价格与运输费在一个神经元的作用下转换为“可负担性”）

最终进入输出层并给出结果（逻辑运算，这一步的算法取决于输出的需要是什么结果，例如二分法就可以用 sigmoid 函数）。层数=隐藏 + 输出，

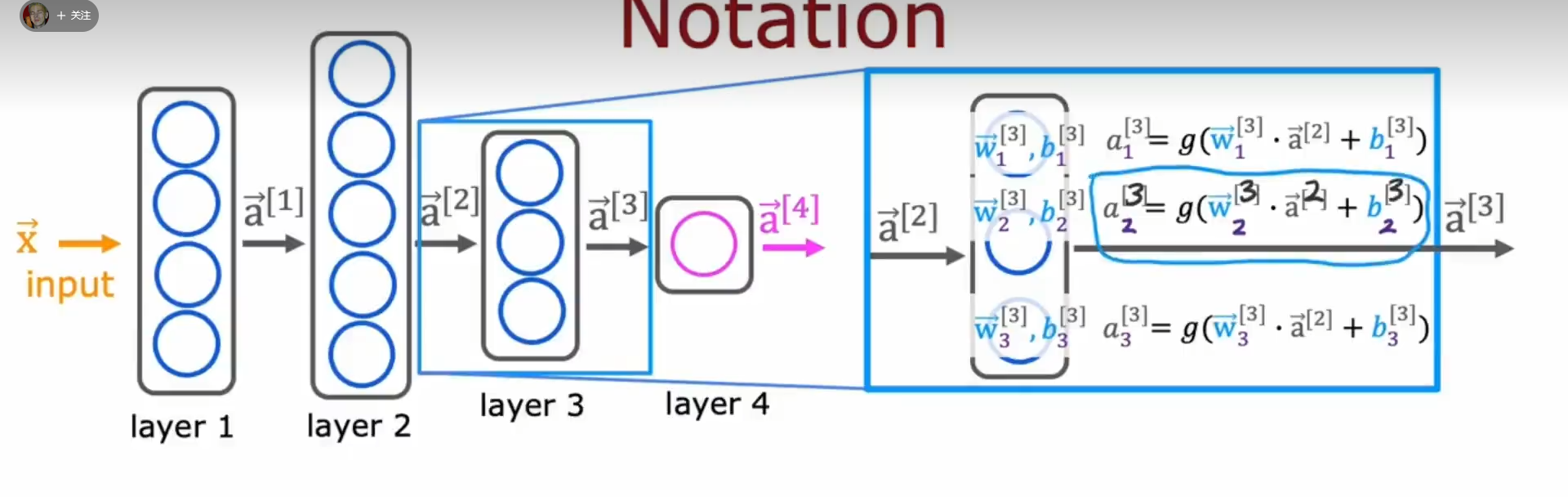
上下标理解：如图层 3，w b 是第三层的参数，第一个 a 是第三层的输出值也是第四层的输入，第二个 a 是第二层的输出也是第三层的输入，下标代表第几个神经元

前向传播：神经元减少

多标签分类：对于某一组输入值需要进行多个二元判断，如有无汽车，有无单车，输出一个 01 数组

多成本分类：对于某一组输入值需要判断他的类型吗，如可以是汽车，单车，行人而非输出是与不是

卷积

将图像矩阵二进制化，根据多个特征制作出多个卷积核，矩阵相乘实现卷积化，接下来对数据进行压缩同时避免过拟合的发生（池化），对一个区域内的数据取一个特定的值，最后来到激活层，一般使用 Relu 函数

激活函数

当我们想要神经元根据输入的输出得到不同的输出的时候就需要考虑激活函数的使用

sigmoid 函数

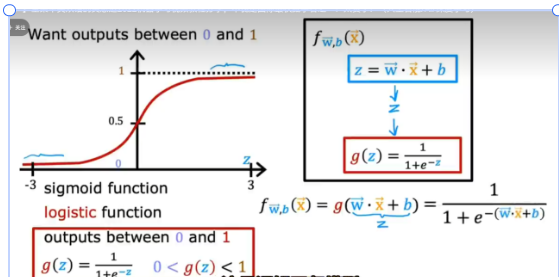
ReLU 函数

隐藏层最多见的激活函数，其运算简单，坡度大便于进行梯度下降

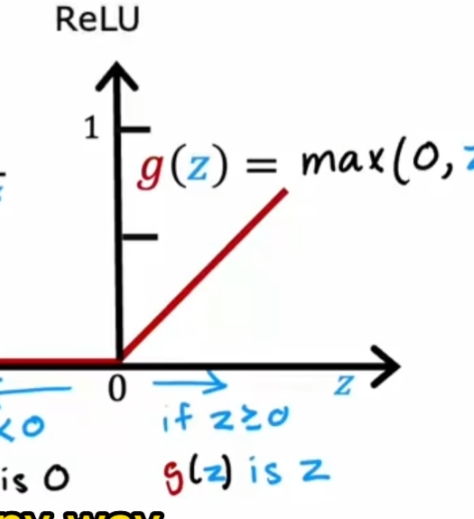
线性激活函数（无激活函数）

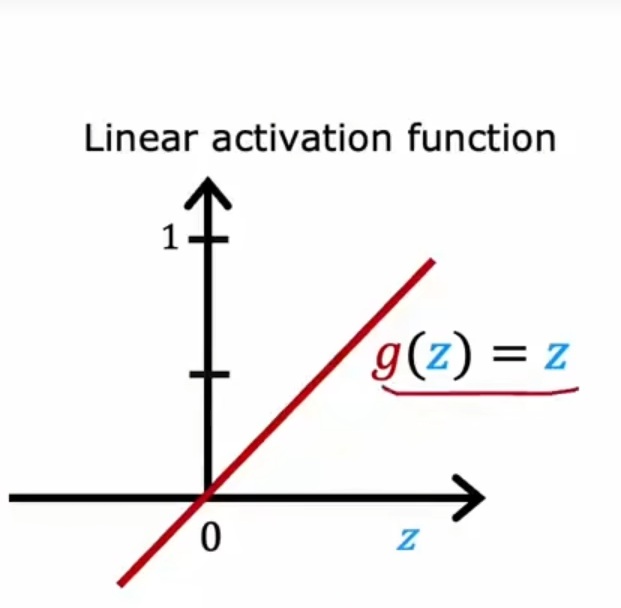
决策树

根节点，决策节点，叶节点

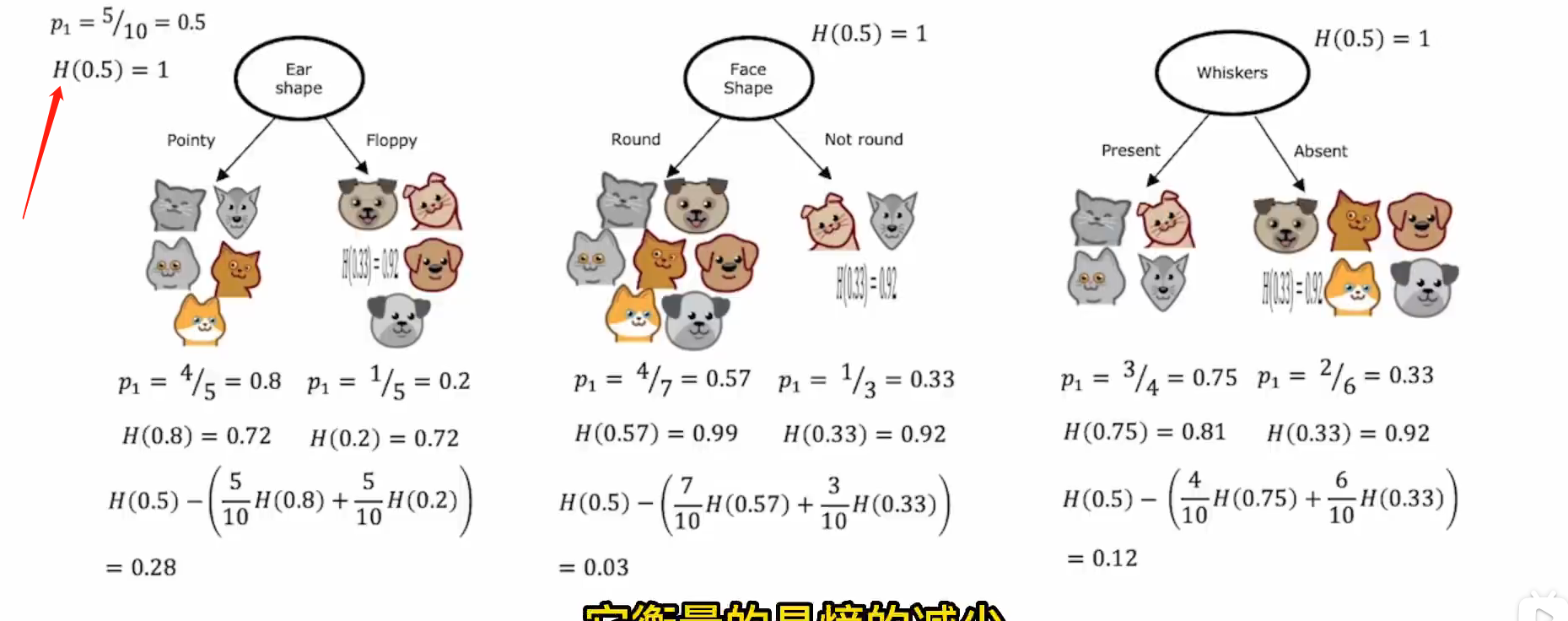
信息增益（熵的减少）

选择减少最多的

P：目标在这个分组中的数目 w：这个分组的总数除以分组前总数

停止

为了避免过度拟合，需要有终止条件

1.完全纯洁

2.限制最大深度

3.信息增益太小（熵减少的少）

4.某个节点例子过少

树集合（Ensembles tree）

由于原本的决策树会受到某个数据的改变而产生巨大变化，则通过不同数据创建多个树

替换：例如在十个样例中，每次抽取一个样例，然后再放回，再在十个之中抽取一个

xgboost：增大下次决策时抽取上次失败的样例的概率

回归树

例如要预测 xx 脸 xx 耳朵动物的体重，则根据方差权重后的差值来选择

无监督学习算法

k-means 聚类算法

在数据集中随机取 n 个点（簇质心），对于所有数据，选择离得最近的点，然后将 n 个点移到最近的点的平均值上，重复以上步骤直到这 n 个点不再变化

代价

代价函数

j 来代表数据与预测值之间的差

平方误差成本函数

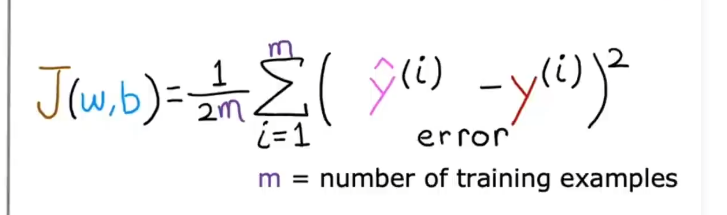
在计算逻辑回归的时候会导致代价函数变成如下，就不能使用梯度下降来得到合理值了

逻辑回归损失函数

也叫 binary cross-entropy function 二进制交叉熵

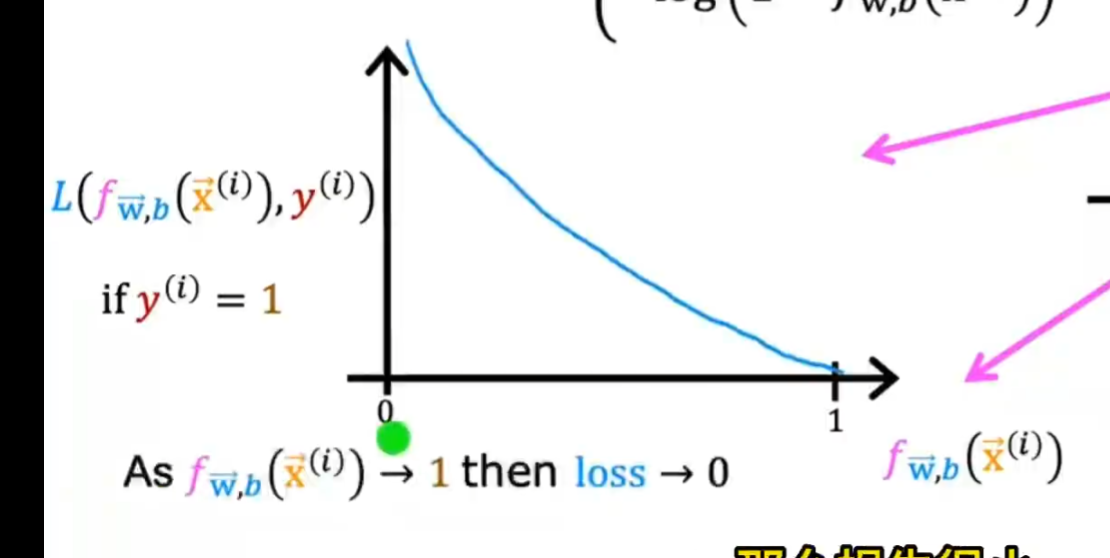
根据预估是 1 还是 0 来选择自己的模型 L 是 loss 函数

例如 y=1，预估值为

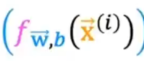
会得到如下函数，越接近 1 计算出来的成本 loss 就会越小，越接近 0loss 越大而且增长率高

softmax 回归损失函数

Sparse categorical cross-entropy 稀疏范畴交叉熵

可以输出多种结果而非二分

与上同理，当 y=1，得到的 a1 越接近 1 损失越小

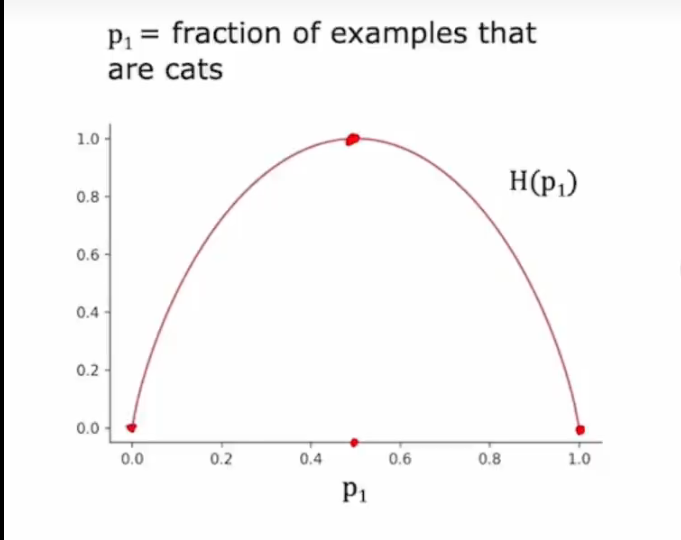
熵

用来衡量纯洁度，越接近百分之五十的时候熵越高，即越不纯洁

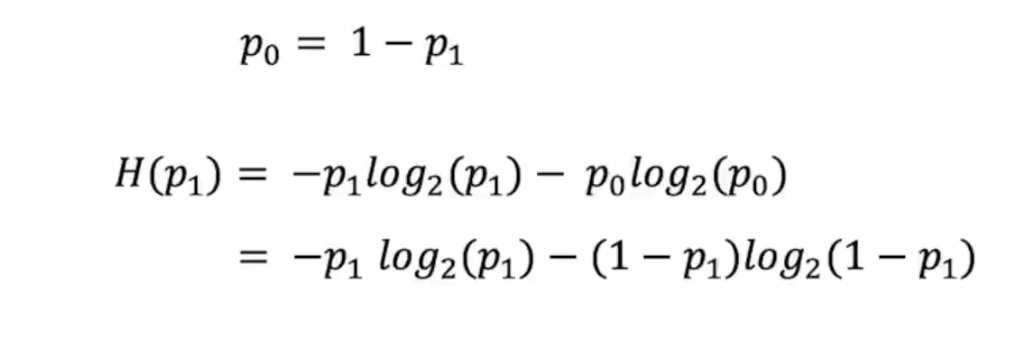
算法

梯度下降

在坡顶找一个下坡最快的位置走上一小步

学习率 α 太高导致跳过最低点，太低导致运行速度慢：寻找最大合理值

偏导数通过斜率来决定这一步走多长，随着接近局部最小值，变化率降低

如何检测是代码错误还是学习率不当？ –> 将学习率设置的非常小来检查

检查是否收敛：j-迭代次数图或者自动收敛测试

亚当算法（优化器）

修改学习率

正规方程

无需迭代，但是只适用于线性回归 速度慢

拟合问题

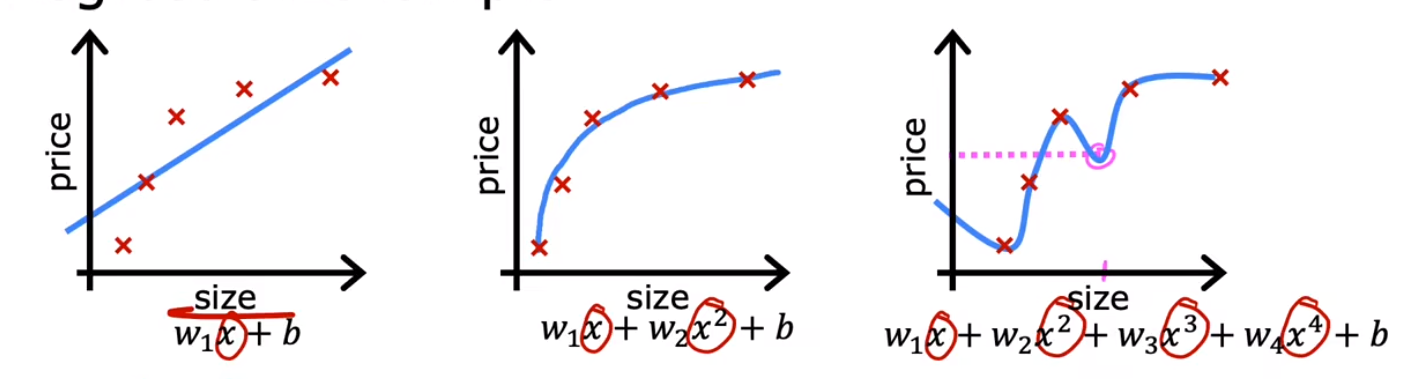
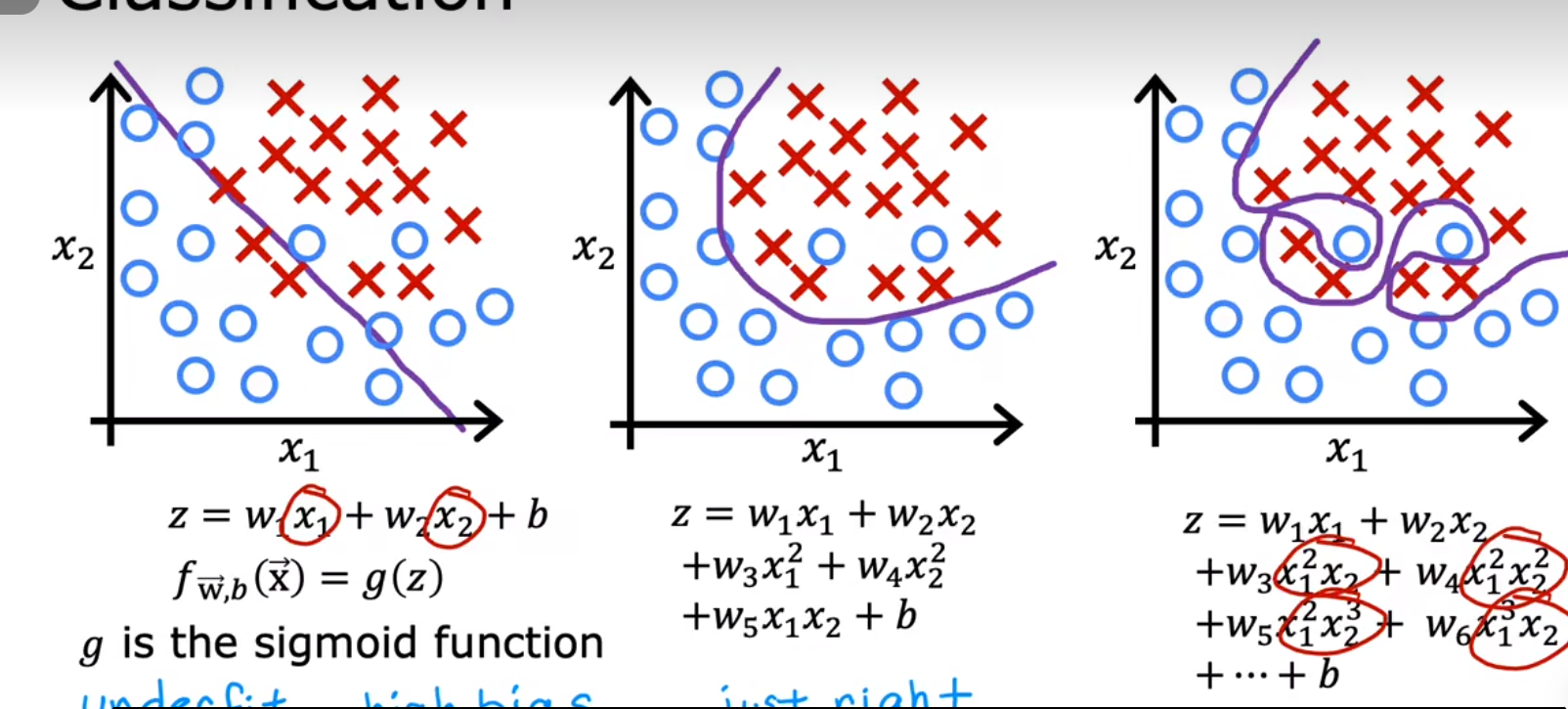
欠拟合（高偏差） high bias

算法不准确

泛化

让算法在处理未测试的数据集的时候仍有优秀的预测

过拟合（高方差） high variance

算法对数据集中所有数据精确处理但是失去了预测的能力

解决方案

特征

减少与增加

多项式回归

改变 x 的次数

增加数据集

一味地增加数据集效果有限，对高方差的效果会好

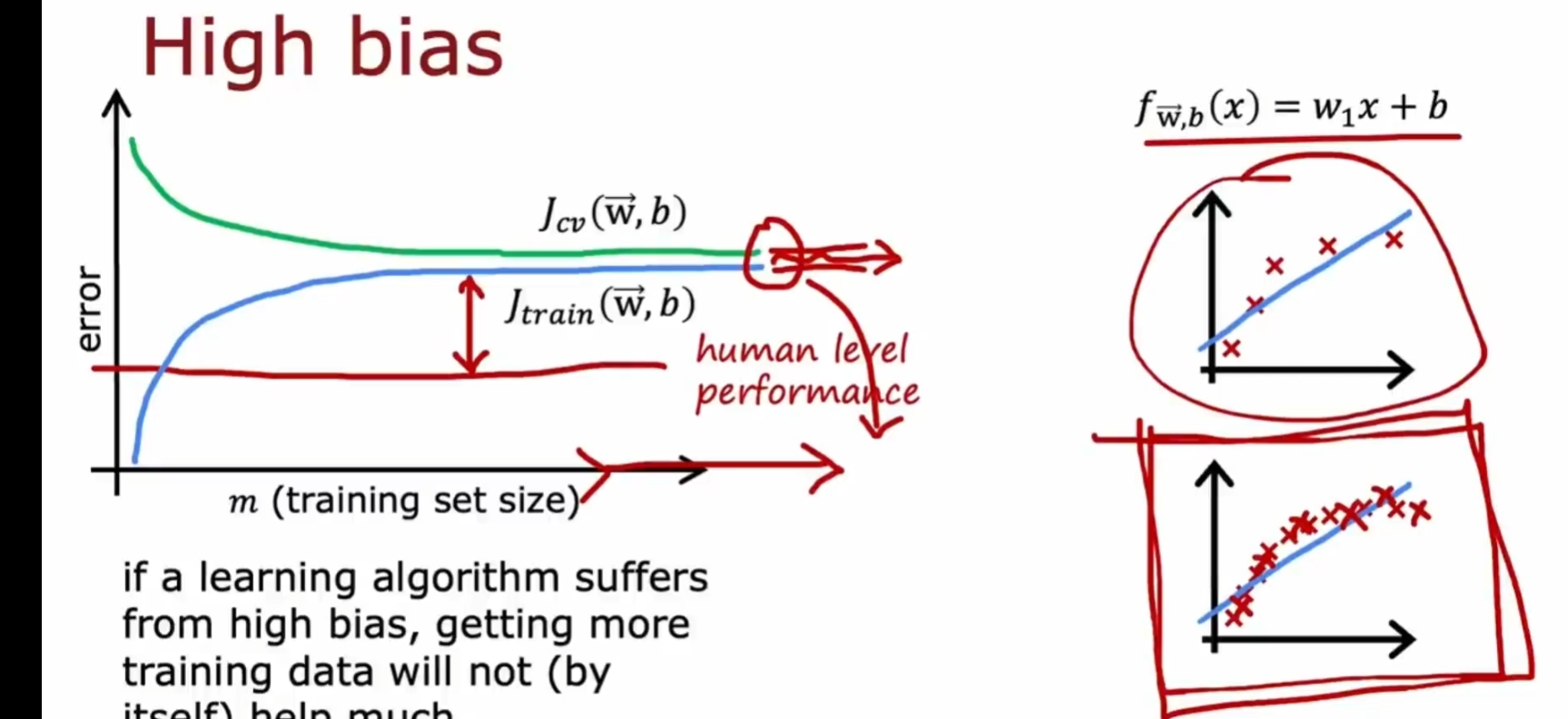
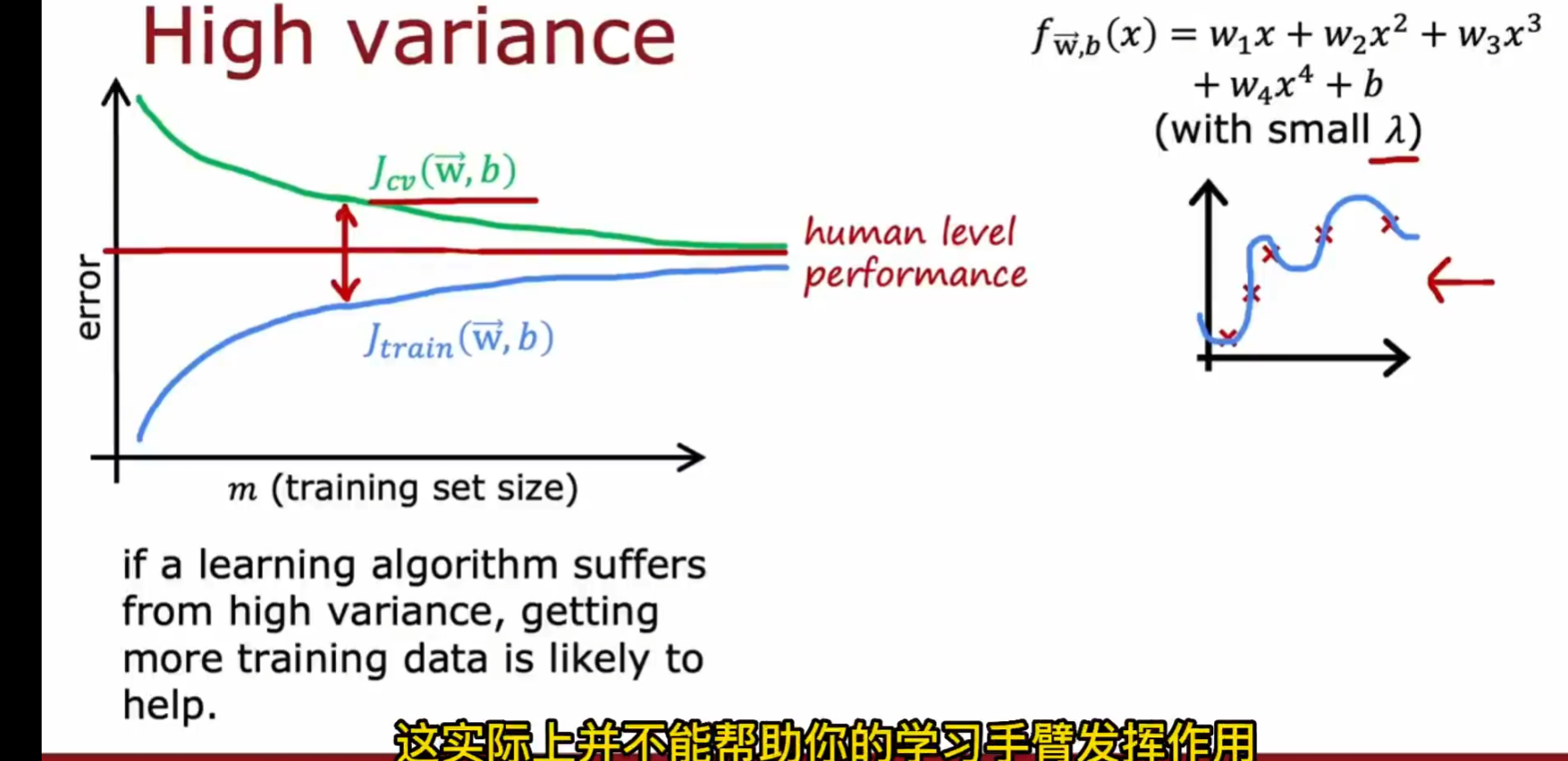
特征选择：减少相关性弱的特征，避免多项式表达能力过强

正则化

保留相关特征，减少权重

使用场景：特征多但是不能确认哪个特征是有用或者无用的 lambda 需要选择合适的大小

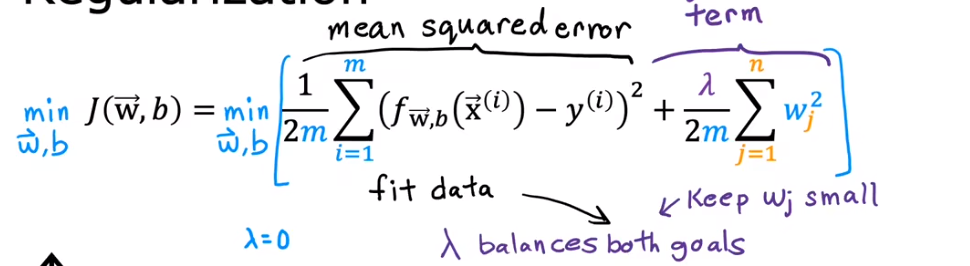
正则化线性回归梯度下降

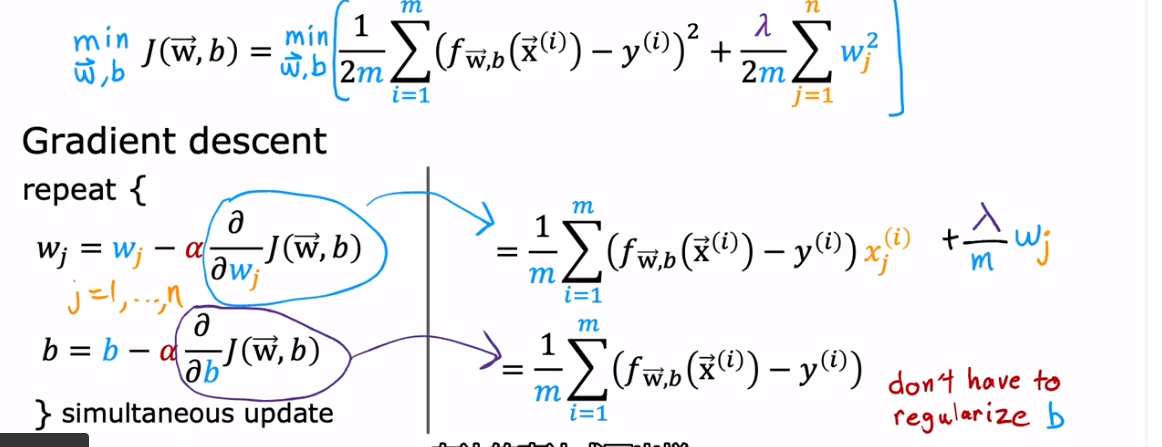
正则化逻辑回归梯度下降

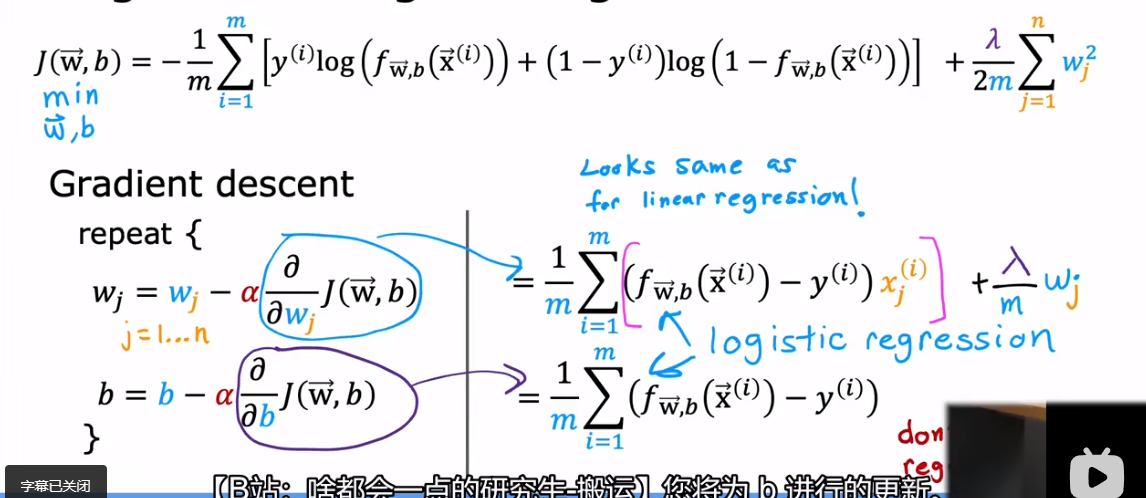
lambda

增大 lambda 导致模型简化

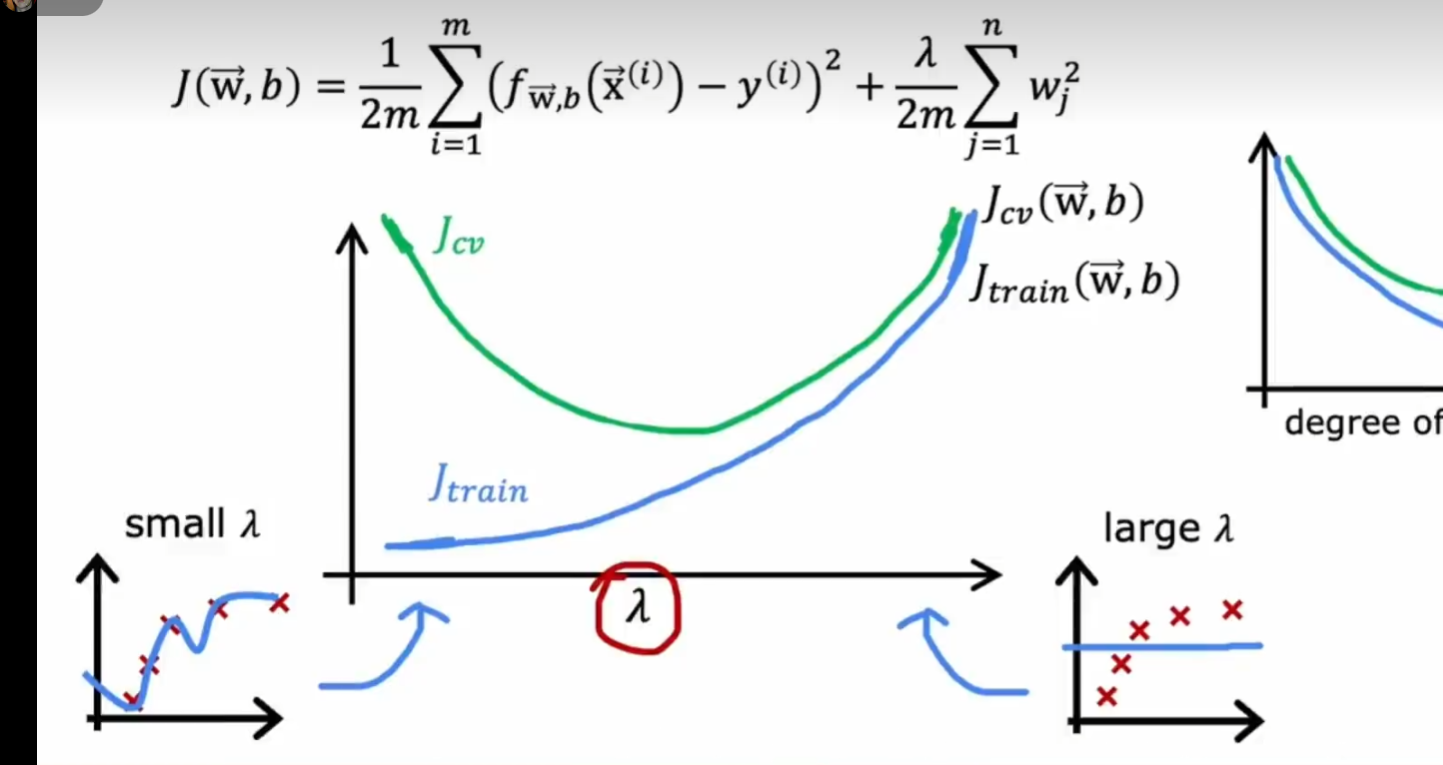
lambda 增大会导致 j train 不断增大（越来越偏离测试集）

lanbda 过大—过拟合 过小—近似常数方程

诊断

训练：得到 j train 和多组已经完成了拟合的参数

选择模型（交叉验证）：得到 j cv 函数查看哪一组参数的误差小然后做出选择

测试：模拟现实情况来评估泛化能力

高偏差：在训练集上存在较大误差

高方差：j cv 远大于 j train 在交叉验证集中的误差远大于训练集上的误差（训练误差小，其他大）

高方差 + 高偏差：j cv 远大于 j train 而且 j train 很高